Aquí encontraras una ficha de Conceptos Previos de las Funciones para Primer Grado de Secundaria o estudiantes que tengan 12 años de edad. Este material educativo lo podrás descargar GRATIS en formato PDF y corresponde al curso de ÁLGEBRA.
Muestra del Material Educativo
En esta parte te mostraremos una muestra de la PRIMERA PÁGINA de la ficha de Conceptos Previos de las Funciones.
Esta ficha de Conceptos Previos de las Funciones para estudiantes de secundaria, estará a tu alcance de forma sencilla y gratuita.
Descarga GRATIS este Material Educativo
Este material educativo de Conceptos Previos de las Funciones estará a tu alcance en formato PDF de forma GRATUITA. Aquí te dejamos los enlaces de descarga, selecciona la opción de tu preferencia:
Opción A – PDF | Opción B – PDF
¿Qué Contiene este Material Educativo que te Ofrecemos?
Este recurso educativo de Par Ordenado que te compartimos, lleva contenidos teóricos importantes como:
- Par Ordenado.
- Definición de Función.
- Actividades para desarrollar.
Ahora te mostraremos algunos de estos conceptos:
Par Ordenado
Es el conjunto formado por dos elementos dispuestos en un determinado orden. Si «a» y «b» son los elementos de un par ordenado, esto se denota de la siguiente manera:
(a;b) donde:
a: primera componente (ubicada en el eje de las abscisas, eje «x»)
b: segunda componente (ubicada en el eje de las ordenadas, eje «y»)
Representación Gráfica de un Par Ordenado
Sobre el plano de la hoja de papel, tomemos 2 rectas numéricas perpendiculares entre si.
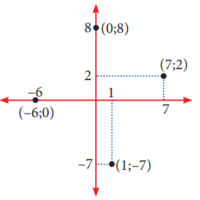
Definición de función
Sean ≪a≫ y ≪b≫ dos conjuntos no vacios (pueden ser A = B) en la que se cumple la siguiente regla de correspondencia.
F = {(x;y) ∈ A × B/∀ x ∈ A; ∃! y ∈ B
«Es decir, para cada elemento de A, le corresponde uno y solo un único elemento de B»
Otras formas de conceptualizar una función
- ≪Es aquella clase especial de relación que posee las 1ras componentes diferentes, no pueden ser iguales≫
F = {(a;b), (c;d), (e;f)} ⇒ a ≠ c ≠ e
- ≪Una función ≪F≫ es un conjunto de pares ordenados, donde no existen dos pares ordenados diferentes con la misma primera componente≫
Si (x;y) ∧ (x;z) ∈ F ⇒ y = z
Actividades de la Ficha de Conceptos Previos de las Funciones
Esta ficha didáctica también contiene actividades de Par Ordenado donde los estudiantes de primero de secundaria podrán resolver, ya sea individualmente o con la ayuda del docente.
Ahora te presentaremos algunas de estas actividades:
1.- Si (2x + 1; y) = (7; 8) Calcula: ≪x . y≫
2.- Si (17; 5) = (x + y; x – y) Calcula: ≪x . y≫
3.- Calcula la suma de elementos del dominio de la funcion: F = {(4; b), (4; 7), (b;5)}
4.- Calcula la suma de elementos del rango de la funcion, si ≪a≫ es minimo F = {(5;a2), (4;a), (5;81)}
5.- Segun la figura, calcula: ≪a – b≫
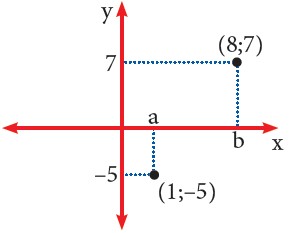
Esperamos que esta separata de Par Ordenado que corresponde al curso de ÁLGEBRA sea de ayuda en la enseñanza y aprendizaje de este maravilloso curso.
Nos encantaría que compartas nuestra página web “materialeseducativos.org” con todos tus amigos y colegas, tenemos una gran variedad de materiales educativos gratuitos.
Más Fichas de Álgebra para Primero de Secundaria
En nuestro sitio web encontraras otras 28 fichas educativas de Álgebra de los temas preparados para estudiantes de Primero de Secundaria, si deseas saber cuales son esos temas y descargar estos materiales educativos, revisa este enlace:
▷ ▷ 28 Fichas de Álgebra para Primer Grado ◁ ◁
Si deseas mas materiales educativos de Álgebra para que puedas descargar gratis en formato PDF y WORD, este enlace te puede interesar:
Otras Fichas de Álgebra de 1er Grado
Déjanos un comentario en la parte de abajo acerca de este material educativo de Álgebra para Primer Grado.
