Aquí podrás descargar GRATIS la ficha de Prisma y Tronco de Prisma para Quinto Grado de Secundaria o estudiantes de 16 años de edad. Este tema se avanza en el curso de GEOMETRÍA y lo podrás descargar en formato PDF.
Muestra del Material Educativo
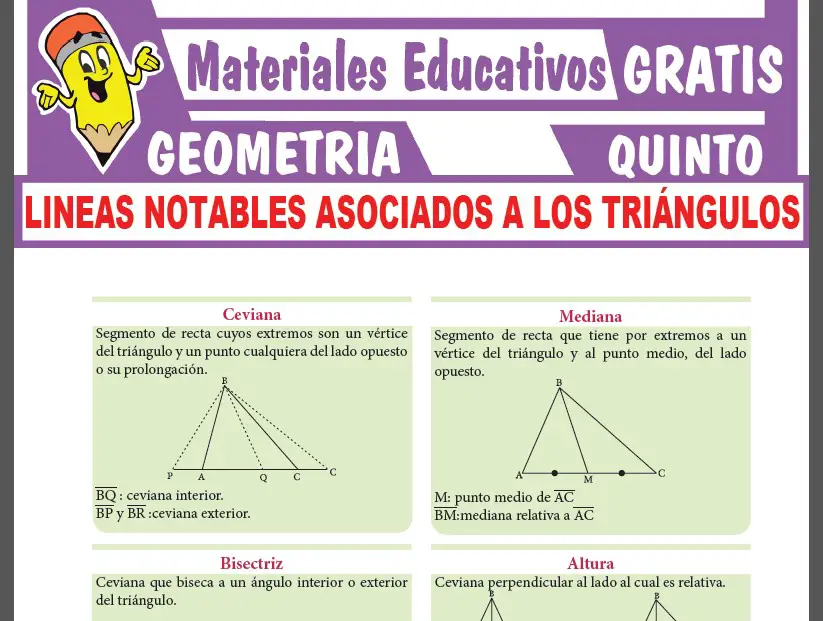
Ahora observaras una pequeña muestra de la 1era PÁGINA de la ficha de Prisma y Tronco de Prisma que te compartimos GRATIS.
 Esperamos que este material educativo de Prisma y Tronco de Prisma te ayude en el aprendizaje y en la enseñanza de las matemáticas.
Esperamos que este material educativo de Prisma y Tronco de Prisma te ayude en el aprendizaje y en la enseñanza de las matemáticas.
Descarga GRATIS este Material Educativo
Esta ficha educativa de Prisma y Tronco de Prisma lo podrás descargar completamente GRATIS en formato PDF a través de los siguientes enlaces:
Opción A – PDF | Opción B – PDF
¿Qué Contiene esta Ficha Educativa que te Ofrecemos GRATIS?
Esta ficha de Clasificación de los Prismas contiene conceptos y formulas muy importantes acerca de:
- Superficie Prismática.
- Clasificación de los Prismas.
- Formulas.
- El Cilindro y Tronco de Cilindro.
- Actividades para desarrollar.
Ahora desarrollaremos los conceptos de algunos de estos contenidos:
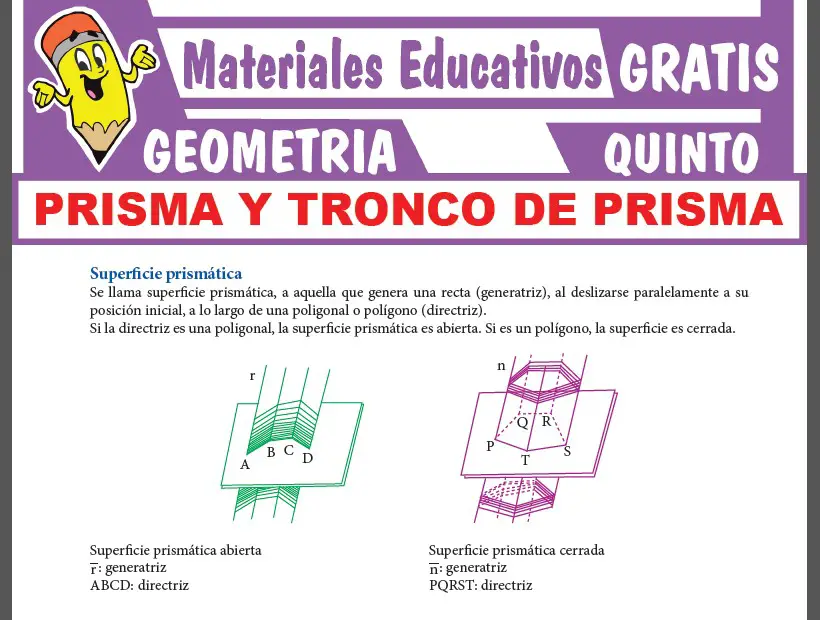
Superficie Prismática
Se llama superficie prismática, a aquella que genera una recta (generatriz), al deslizarse paralelamente a su posición inicial, a lo largo de una poligonal o polígono (directriz). Si la directriz es una poligonal, la superficie prismática es abierta. Si es un polígono, la superficie es cerrada.
Prisma
Un prisma, es el poliedro determinado al interceptar una superficie prismática cerrada, mediante dos planos paralelos entre sí. La figura adjunta muestra un prisma. Las regiones poligonales ABCDE y A’B’C’D’E’ son paralelas y corresponden a los polígonos congruentes.
Estas dos caras son las «bases» del prisma y la distancia entre ellas es la altura del sólido. Las demás caras son regiones paralelográmicas, llamadas «caras laterales»; sus intersecciones se llaman «aristas paralelas». Todas las aristas laterales son paralelas y congruentes.
Clasificación de los Primas
Se clasifican en: recto, oblicuo y regular
Prisma Recto
Es aquel cuyas aristas laterales son perpendiculares a las bases. Las caras laterales son regiones rectangulares, y las aristas laterales son congruentes a la altura.
Prisma Oblicuo
Tiene sus aristas laterales oblicuas a las bases. Según sus bases sean regionales triangulares, cuadrangulares, pentagonales, etc, los primas se llaman triangulares, cuadrangulares, pentagonales, etc. Por ejemplo, la figura (a) muestra un prisma recto triangular.
Prisma Regular
Aquel prisma recto, cuyas bases corresponden a polígonos regulares. (En cualquier otro caso, el prisma no es regular).
Paralelepípedo
Aquel prisma cuyas bases son regiones paralelográmicas.
Clasificación de paralelepípedos
Se clasifican en:
- Paralelepípedo recto: sus aristas laterales son perpendiculares a las bases. Las caras laterales son regiones rectangulares.
- Paralelepípedo: tiene sus aristas laterales oblicuas a las bases. Las seis caras son regiones paralelográmicas.
- Paralelepípedo rectangular: aquel paralelepípedo recto cuyas bases son regiones rectangulares. Llamado también rectoedro.
- Cubo: es un paralelepípedo rectangular que tiene todas sus aristas congruentes.
- Romboedro: aquel paralelepípedo que tiene por bases regiones romboédricas.
Fórmulas
Estos son los siguientes:
Superficie lateral y total de un prisma
La superficie lateral de un prisma es la suma de las superficies de todas sus caras laterales. La superficie total del prisma es la suma de superficie material y de las dos bases. A dichas superficies se refieren las áreas lateral y total.
Volumen de un prisma
El volumen de un prisma es el producto del área de una base por su altura. También, el volumen de un prisma, es el producto del área de una sección recta por una arista lateral.
Tronco de primas
Se obtiene al interceptar la superficie lateral de un prisma, con plano no paralelo a las bases.
Las caras laterales son trapecios.
- El volumen es igual al producto del área de una sección recta y la longitud del segmento que une los centros de gravedad de las bases del tronco (CG’). (Las secciones rectas del tronco son las mismas que el prisma original).
- Existen fórmulas sencillas para evaluar el volumen de un tronco de prisma de base triangular.
Cilindro y Tronco de Cilindro
Comprende lo siguiente:
Superficie cilíndrica
Es la superficie generada, al deslizarse una recta (generatriz), a lo largo de una curva, (directriz), manteniéndose paralela a su posición inicial.
Cilindro
Es el sólido obtenido al interceptar una superficie cilíndrica cerrada, por medio de dos planos paralelos. Las regiones que determinan dichos planos, son las bases del cilindro y la distancia entre ellos es la altura.
Cilindro de revolución
Se genera al girar una región rectangular, una vuelta, alrededor de un eje que contiene a un lado. Las bases son círculos y la altura mide igual que la generatriz. Es también llamado cilindro circular recto.
Desarrollo de la superficie lateral
Es la región rectangular, obtenida al extender (desarrollar) la superficie lateral, de modo que los lados del rectángulo sean la generatriz y las circunferencias de las bases, del cilindro de revolución original.
Tronco de cilindro
Se obtiene al intersectar la superficie lateral de un cilindro, con un plano no paralelo a las bases.
Ejercicios de la Ficha de Prisma y Tronco de Prisma
En esta ficha educativa también encontraras muchos problemas y ejercicios de Clasificación de los Prismas preparadas de forma especial para los estudiantes de 5to de secundaria.
Ahora te presentaremos algunos de estos ejercicios:
1.- Calcula el volumen del prisma recto.

2.- Calcula el área de la superficie lateral del prisma regular.

3.- Calcula el área de la superficie lateral del prisma recto.

4.- Calcula el volumen del sólido.

5.- Dado un prisma recto cuya base es un hexágono regular inscrito en una circunferencia de diámetro 8 m y cuya altura es igual en longitud al diámetro. Calcula el volumen del prisma.
Estos ejercicios y problemas de Clasificación de los Prismas fueron planteados por un equipo de docentes especialistas de esta área (Geometría), por lo que recomendamos a los estudiantes que desarrollen todos estos problemas propuestos.
Te invitamos a seguir navegando en nuestra web: “materialeseducativos.org”, tenemos una gran variedad de materiales educativos de todos los cursos y para todos los grados.
Más Fichas de Geometría para Quinto de Secundaria
En este sitio web educativo encontraras otras 28 fichas educativas de Geometría de los demás temas preparados para estudiantes de Quinto de Secundaria, si deseas conocer los temas que te ofrecemos, puedes revisar el siguiente enlace:
▷ ▷ 28 Fichas de Geometría para Quinto Grado ◁ ◁
Si deseas mas materiales educativos de Geometría para que descargues de manera gratuita en formato PDF y WORD, puedes revisar el siguiente enlace:
Otras Fichas de Geometría de 5to Grado
Puedes dejarnos un comentario en la parte de abajo acerca de este material educativo de Geometría para Quinto Grado.