Aquí encontraras la ficha de Relaciones entre Conjuntos para Segundo Grado de Secundaria o estudiantes que tengan 13 años de edad. Este material educativo corresponde al curso de ARITMÉTICA y lo podrás descargar GRATIS en formato PDF.
Muestra del Material Educativo
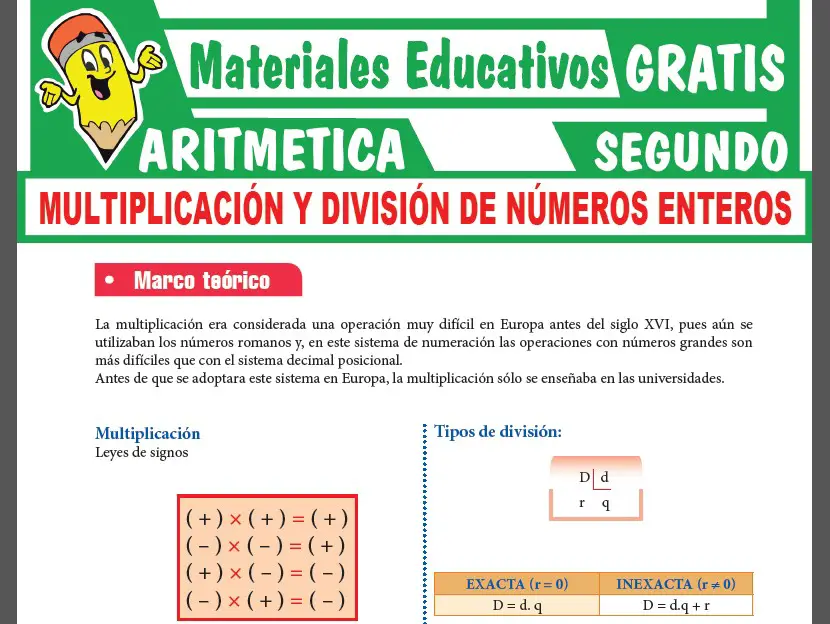
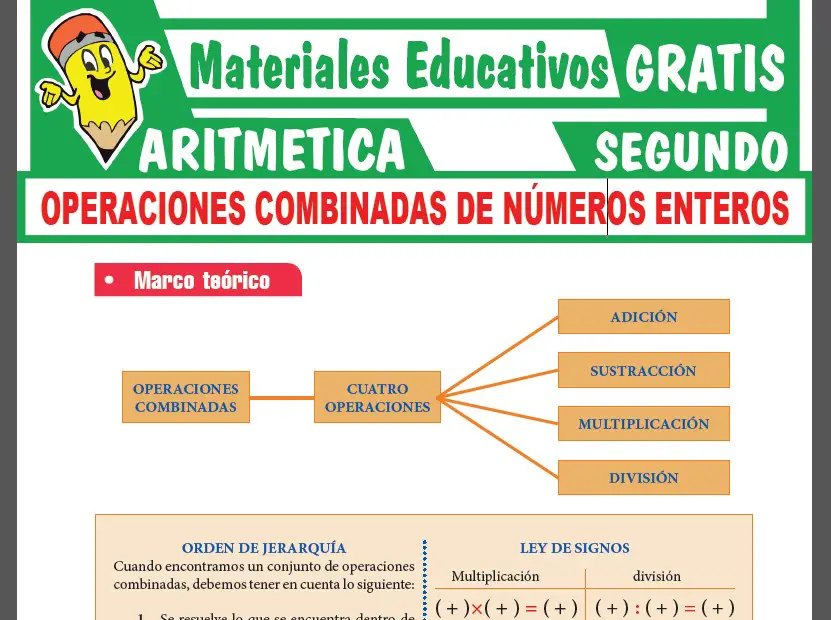
En esta parte veras una muestra de la 1era PÁGINA de la ficha de Relaciones entre Conjuntos.
Para obtener este increíble material educativo de Relaciones entre Conjuntos solo bastara un click, en los enlaces que te presentaremos a continuación:
Descarga GRATIS esta Ficha Educativa
Aquí podrás descargar este maravilloso material educativo de Relaciones entre Conjuntos que fue elaborado para estudiantes de segundo de secundaria.
Opción A – PDF | Opción B – PDF
¿Qué Contiene esta Ficha Educativa que te Ofrecemos?
Esta ficha educativa de relaciones y operaciones entre conjuntos que te compartimos contiene temas que muy importantes como:
- Relación de inclusión.
- Igualdad entre conjuntos.
- Conjunto potencia
- Operaciones entre conjuntos
- Actividades para desarrollar.
Ahora te presentaremos algunos de estos conceptos:
Relación de Inclusión (⊂)
Un conjunto está incluido, contenido o es subconjunto de otro, si todos los elementos del primero son elementos del segundo. Se denota por ⊂ que se lee está incluido, en caso contrario por ⊄.
La inclusión es una relación que se da solo ENTRE CONJUNTOS.
Ejemplo:
A = {1; 2} y B = {1; 2; 3; 4} entonces A ⊂ B
Y se lee:
- A está incluido en B,
- A está contenido en B
- A es subconjunto de B.
OJO:
- El conjunto vacío o nulo está incluido en todo conjunto.
Igualdad Entre Conjuntos
Dos conjuntos A y B son iguales, si A y B tienen los mismos elementos.
Ejemplo:
Dados los conjuntos A = {a; m; o; r} y B = {r; o; m; a}
- Por lo tanto A = B.
Conjunto Potencia (P(A))
Dado un conjunto A, llamaremos potencia del conjunto A, al conjunto formado por todos los subconjuntos del conjunto A. Se representa P(A).
- Número de subconjuntos de A = 2n(A)
- Número de subconjuntos propios = 2n(A) – 1
Operaciones entre Conjuntos
Unión o reunión (∪)
Ejemplo:
A = {1; 2; 3; 4; 5} y B = {5; 6; 7}, entonces:
- A ∪ B = {1; 2; 3; 4; 5; 6}
Intersección (∩)
Ejemplo:
A = {1; 2; 3; 4; 5} y B = {4; 5; 6; 7}, entonces:
- A ∩ B = {4; 5}
Diferencia (–)
Ejemplo:
A = {1; 2; 3; 4; 5} y B = {4; 5; 6; 7}, entonces:
- A – B = {1; 2; 3} y B – A = {6; 7}
Diferencia simétrica (Δ)
- A ∆ B = (A ∪ B) – (A ∩ B)
Ejemplo:
A = {1; 2; 3; 4; 5} y B = {4; 5; 6; 7}, entonces:
- A ∆ B = {1; 2; 3; 6; 7}
Intersección (∩)
Ejemplo:
U = {1; 2; 3; 4; 5; 6; 7; 8; 9} y B = {2; 4; 6; 8}, entonces:
- B’ = {1; 3; 5; 7; 9}
Actividades de la Ficha de Relaciones entre Conjuntos
En esta ficha educativa también encontraras ejercicios de relaciones y operaciones entre conjuntos que los estudiantes de segundo grado de secundaria podrán resolver con la ayuda del docente o padre de familia.
Estos son algunos enunciados de ejercicios de la ficha:
- Si los conjuntos A y B son iguales, determina x + y: A = {3x + 2; 5y}, B = {30; 29} (x e y son enteros)
- Si los conjuntos P y Q son iguales, además a y b son enteros. Determina a + b: P = {2a + 1; 4b} y Q = {19; 32}
- Un conjunto A tiene 16 subconjuntos. Si n(A) x n(C) = 24, ¿cuántos subconjuntos tiene C?
- En un avión hay 150 personas, de las cuales 60
fuman y 90 beben. ¿Cuántas personas hay que fuman y beben si se sabe que hay 10 personas que
solamente fuman? - En un avión hay 180 personas, de las cuales 80 fuman y 100 beben. ¿Cuántas personas hay que fuman y beben si se sabe que hay 50 personas que solamente beben?
- De 500 integrantes de un club deportivo, 200 se inscribieron en karate y 340 en boxeo. Si 50 no se inscribieron en ninguna de las dos disciplinas, ¿cuántos se inscribieron en ambas disciplinas?
- De los deportistas de la plana de aritmética se supo que 9 practican fútbol y natación, 5 no practican estos deportes, 20 practican solamente natación y 13 practican fútbol. ¿Cuántos deportistas hay en dicha plana?
- Cynthia desayuna jamón o queso cada mañana del mes de noviembre. Si come jamón 15 mañanas y queso 22 mañanas, ¿cuántas mañanas comió queso y jamón?
Este tema de relaciones y operaciones entre conjuntos corresponde al curso de ARITMÉTICA y fue creado especialmente para estudiantes de segundo de secundaria.
En nuestra página web “materialeseducativos.org” contamos con más fichas educativas de este y otros curso y para todos los grados, te invitamos a revisarlos y descargarlos.
Más Fichas de Aritmética para Segundo de Secundaria
En nuestra pagina web también podrás encontraras otras 28 fichas de Aritmética para estudiantes de segundo de secundaria, aquí le dejamos el enlace para que lo puedas revisar:
▷ ▷ 28 Fichas de Aritmética para Segundo Grado ◁ ◁
Si necesita mas materiales educativos de aritmética para estudiantes de este mismo grado, en seguida te compartiremos el enlace de otro sitio web educativo que también te ofrece materiales educativos gratuitos de aritmética, este es su enlace:
Otras Fichas de Aritmética de 2do Grado
¿Que te pareció esta ficha educativa de aritmética para segundo grado?, coméntanos abajo (en la caja de comentarios).
