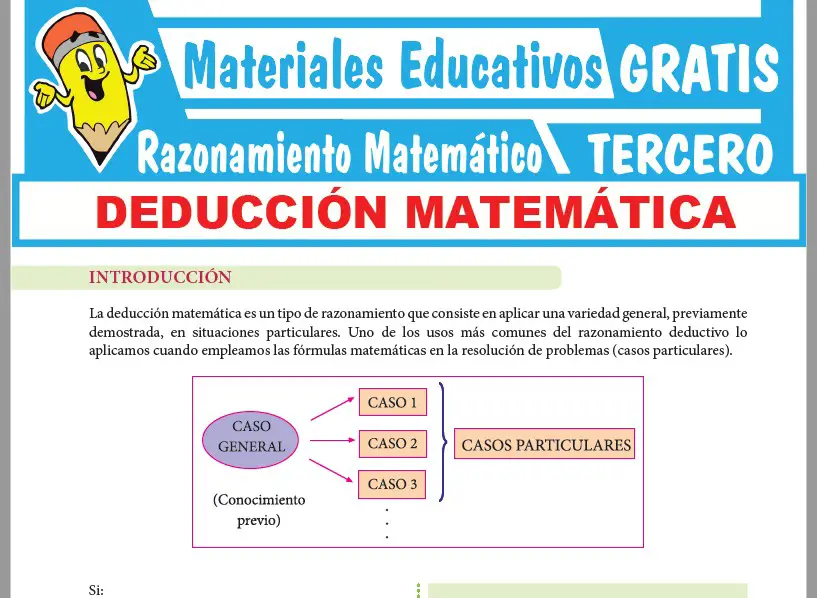
Aquí encontraras la ficha de Principios del Análisis Combinatorio para Tercer Grado de Secundaria o estudiantes que tengan 14 años de edad. Este contenido se desarrolla en el curso de RAZONAMIENTO MATEMÁTICO y lo podrás descargar GRATIS en formato PDF.
Muestra del Material Educativo
Ahora observaras una muestra de la PRIMERA PÁGINA de la ficha de Principios del Análisis Combinatorio que podrás descargar más abajo.
Este recurso educativo de Principios del Análisis Combinatorio lo podrás adquirir sin realizar ningún tipo de pago, esperamos que sea de mucha utilidad.
Descarga GRATIS este Material Educativo
En esta parte usted podrá descargar este increíble material educativo de Principios del Análisis Combinatorio que fue preparado exclusivamente para estudiantes de tercero de secundaria.
Opción A – PDF | Opción B – PDF
¿Qué Contiene este Material Educativo que te Ofrecemos?
En esta ficha de Análisis Combinatorio encontraras contenidos teóricos muy importantes como:
- Principios de adición
- Principios de multiplicación
- Factorial de un número
- Permutacion lineal
- Permutacion Circular
- Actividades para desarrollar.
Ahora te mostraremos parte del contenido que encontraras en la ficha educativa que te ofrecemos.
Principio de Adición
Supongamos que una persona desea viajar de Lima a Tumbes. Para ello dispone de 2 líneas aéreas, 3 líneas terrestres y 1 ruta marítima. ¿De cuántas maneras distintas puede viajar esta persona? Teniendo en cuenta, claro, que el viaje solamente lo podemos realizar por una sola vía.
Conclusión:
Si va por avión, tiene 2 formas diferentes de viajar, si va vía terrestre tiene 3 formas más y si va por mar, una forma más; en total, tendría 6 formas de realizar el viaje.
Principio de Multiplicación
Supongamos que Ruth recibe como regalo de cumpleaños 1 falda morada, una dorada y otra blanca; también recibe una blusa celeste y otra roja. Si ella desea probarse las prendas recibidas. ¿De cuántas maneras distintas puede exibirlas, si s epone blusa y falda a la vez?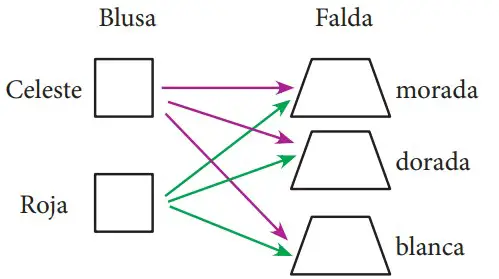
Factorial de un Número
La factorial de un número «n» entero y positivo, denotado por n! o Ln es el producto de todos los números enteros y consecutivos desde la unidad hasta el valor de «n».
Ejemplo:
- 3! = 3 × 2 × 1 = 6
- 6! = 3! × 4 × 5 × 6 = 720
En general:
- n! = n(n – 1)(n – 2)… × 3 × 2 × 1
Permutación Lineal
Es un arreglo de ordenación de todos los elementos de un conjunto ordenado de forma lineal.
Permutación de A y B
- AB; BA ⇒ 2 permutaciones
Permutación de A, B y C
- ABC; BCA; CAB; ACB; BAC; CBA 6 permutaciones
Para «n» objetos diferentes, el número de permuaciones, representado como Pn se podrá obtener con:
- Pn = n! = n(n – 1)(n – 2)… × 3 × 2 × 1
Permutación Circular
Es un arreglo que se puede hacer con los elementos de un conjunto alrededor de un objeto (o centro) señalado. El número de permutaciones circulares, denotado como «Pc» de «n» elementos, está dado por:
- Pc = (n – 1)!
Actividades de la Ficha de Principios del Análisis Combinatorio
Después del contenido teórico, este material educativo contiene muchas actividades de Análisis Combinatorio elaborados especialmente para los estudiantes del tercer grado de secundaria. Dichas actividades las podrán desarrollar los estudiantes de forma individual o con la ayuda del docente.
Estas son algunas de las actividades:
- Eufrasio planea ir de viaje a Trujillo para ello tiene a su disposición 5 líneas aéreas y 8 líneas terrestres. ¿De cuántas maneras podrá hacer su viaje?
- Rufino tiene 7 polos y 5 pantalones. Si todas sus prendas son de diferente color, ¿de cuántas maneras distintas podrá vestirse Rufino?
- ¿Cuántas permutaciones pueden formarse con las letras a; b; c; d y e?
- ¿Cuántas permutaciones pueden formarse con los números 1; 2; 3 y 4?
- Sin importar el significado o si tienen sentido o no. ¿Cuántas palabras distintas se podrán formar con todas las letras de la palabra COLEGIO?
- Con las cifras 1; 3; 5; 7 y 4. ¿Cuántos números pares de tres cifras diferentes se pueden formar?
- Si alrededor de una torta de cumpleaños se ubican seis vasos diferentes, ¿de cuántas formas podrán ser ubicados dichos vasos?
- Si tres señoritas y 4 jóvenes juegan a la ronda, ¿de cuántas maneras distintas podrán hacerlo si las señoritas siempre quieren estar juntas?
Esperamos que por medio de este material educativo los estudiantes de tercero de secundaria aprendan este importante tema de Análisis Combinatorio que pertenece al curso de RAZONAMIENTO MATEMÁTICO.
Si te gusto este material educativo te invitamos a compartirlos con todos tus amigos y colegas.
Más Fichas de Razonamiento Matemático para Tercero de Secundaria
En nuestra pagina educativa tenemos mas fichas educativas de razonamiento matemático para estudiantes de Tercero de Secundaria, puedes revisarlos en el siguiente enlace:
▷ ▷ 28 Fichas de Razonamiento Matemático para Tercer Grado ◁ ◁
Y si deseas otras fichas de trabajo de razonamiento matemático para estudiantes de este mismo grado, ahora te dejamos el enlace que corresponde a otra pagina educativa que también ofrece materiales educativos gratuitos, este es su enlace:
Otras Fichas de Raz. Matematico de 3er Grado
«¿Que opinas de esta ficha de Razonamiento Matemático de tercer grado?, déjanos tu comentario en la parte de abajo«
