Aquí encontraras la ficha de La Circunferencia y sus Propiedades para estudiantes que tengan 13 años de edad o que se encuentren en Segundo Grado de Secundaria. Este material educativo pertenece al curso de GEOMETRÍA y lo podrás descargar GRATIS en formato PDF.
Muestra del Material Educativo
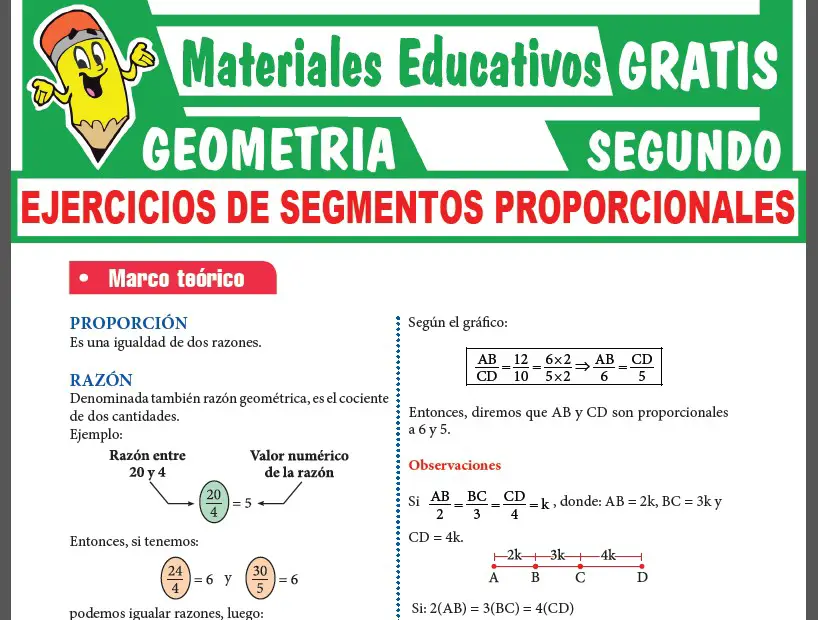
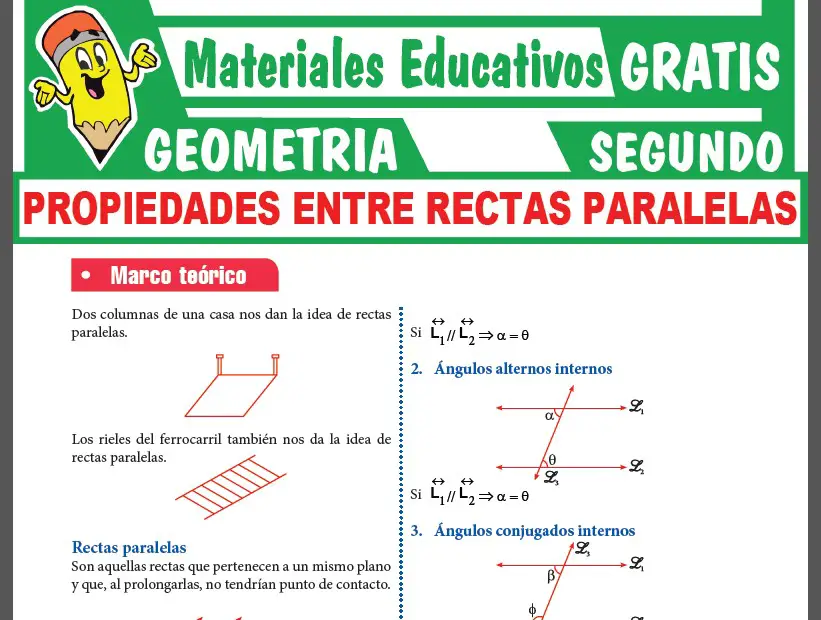
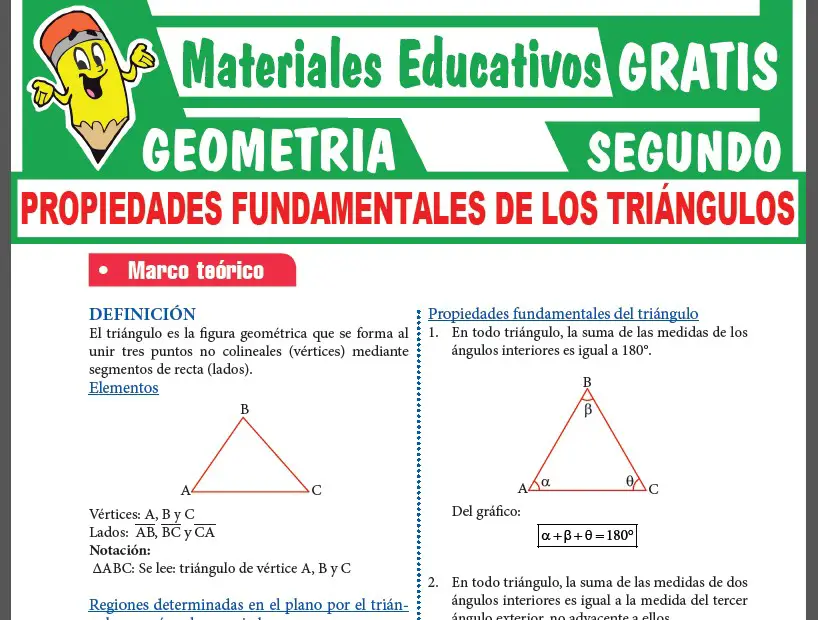
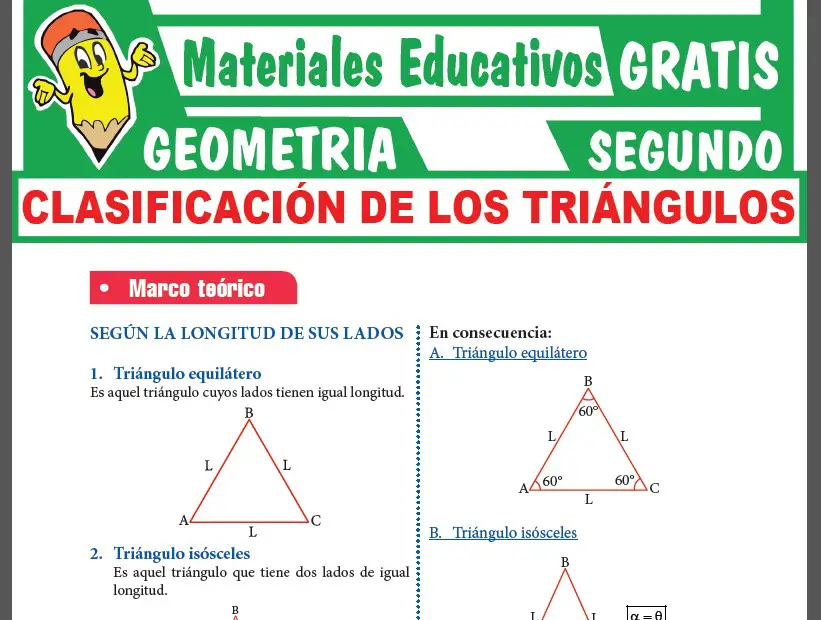
Ahora observaras una muestra de la 1era PÁGINA de la ficha de La Circunferencia y sus Propiedades.
Deseamos que este material educativo de La Circunferencia y sus Propiedades contribuya al aprendizaje de la geometría.
Descarga GRATIS esta Ficha Educativa
En esta parte te dejaremos los enlaces para que puedas descargar este maravilloso material educativo de La Circunferencia y sus Propiedades que fue preparado para estudiantes de segundo de secundaria.
Opción A – PDF | Opción B – PDF
¿Qué Contiene esta Ficha Educativa que te Ofrecemos?
Esta ficha didáctica de Propiedades de la Circunferencia que te ofrecemos contiene los siguientes temas:
- Circunferencias.
- Propiedades da la Circunferencia.
- Teorema de Poncelet.
- Actividades para desarrollar.
Ahora te presentaremos algunos de sus conceptos:
La Circunferencia
Es el conjunto de puntos de un plano, que equidistan de otro llamado centro «O», donde OA se llama radio.
Propiedades
- En toda circuferencia, el radio que interseca a una recta tangente en el punto de tangencia, forma un ángulo recto con la recta.
- En toda circunferencia, el radio que es perpendicular a toda cuerda, la biseca. Y también biseca al arco que define la cuerda sobre la circunferencia.
- En una circunferencia, en la que se han trazado 2 cuerdas de la misma longitud, estas determinan arcos de igual medida.
- En toda circunferencia, los segmentos tangentes trazados desde un punto exterior tienen la misma longitud.
- En toda circunferencia, las cuerdas paralelas determinan arcos de igual medida entre las paralelas.
Teorema de Poncelet
En todo triángulo rectángulo, la suma de longitudes de los catetos es igual a la longitud de la hipotenusa más el doble del inradio.
Teorema de Pitot
En todo cuadrilátero circunscrito a una circunferencia, la suma de las longitudes de los lados opuestos es constante.
Ejercicios de la Ficha de La Circunferencia y sus Propiedades
En esta ficha también encontraras ejercicios de Propiedades de la Circunferencia donde los estudiantes podrán resolver poniendo en práctica las propiedades y fórmulas de este tema.
Ahora te presentaremos algunos de estos ejercicios:
1.- Calcula «x» si R = 3 m (A y B: puntos de tangencia)
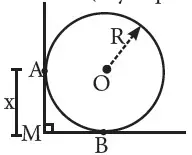
2.- Si R = 13 m y la distancia de O hacia AB es 5 m, calcula AB.
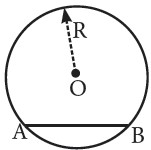
3.- Calcula «x», si A y B son puntos de tangencia.
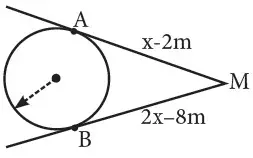
4.- Calcula «x» si BC = 6 m, además M, N y P son puntos de tangencia.
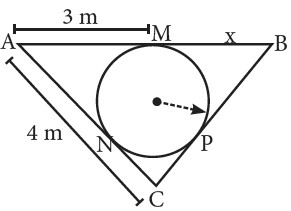
5.- Calcula «x» si AB = 4u y BC = 3u.
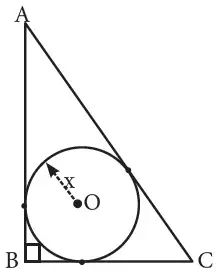
Este tema de Propiedades de la Circunferencia pertenece al curso de GEOMETRÍA y fue elaborado de forma especial para estudiantes de segundo de secundaria.
En nuestra página web “materialeseducativos.org” contamos con más fichas educativas de todos los curso y para todos los grados de secundaria.
Más Fichas de Geometría para Segundo de Secundaria
En nuestro sitio web encontraras otras 28 fichas educativas de Geometría de otros temas preparados para estudiantes de Segundo de Secundaria, si deseas saber el listado de temas y descargar estos materiales educativos, revisa el siguiente enlace:
▷ ▷ 28 Fichas de Geometría para Segundo Grado ◁ ◁
Si deseas mas materiales educativos de Geometría para que descargues de manera gratuita en formato PDF y WORD, puedes revisar el siguiente enlace:
Otras Fichas de Geometría de 2do Grado
Puedes dejarnos un comentario en la parte de abajo acerca de este material educativo de Geometría para Segundo Grado.
