Aquí podrás descargar GRATIS la ficha de Poliedros Regulares para Quinto Grado de Secundaria o estudiantes de 16 años de edad. Este tema se avanza en el curso de GEOMETRÍA y lo podrás descargar en formato PDF.
Muestra del Material Educativo
Ahora observaras una pequeña muestra de la 1era PÁGINA de la ficha de Poliedros Regulares que te compartimos GRATIS.
Esperamos que este material educativo de Poliedros Regulares te ayude en el aprendizaje y en la enseñanza de las matemáticas.
Descarga GRATIS este Material Educativo
Esta ficha educativa de Poliedros Regulares lo podrás descargar completamente GRATIS en formato PDF a través de los siguientes enlaces:
Opción A – PDF | Opción B – PDF
¿Qué Contiene esta Ficha Educativa que te Ofrecemos GRATIS?
Esta ficha de Clases de Poliedros contiene conceptos y formulas muy importantes acerca de:
- Poliedro.
- Clases de Poliedros.
- Actividades para desarrollar.
Ahora desarrollaremos los conceptos de algunos de estos contenidos:
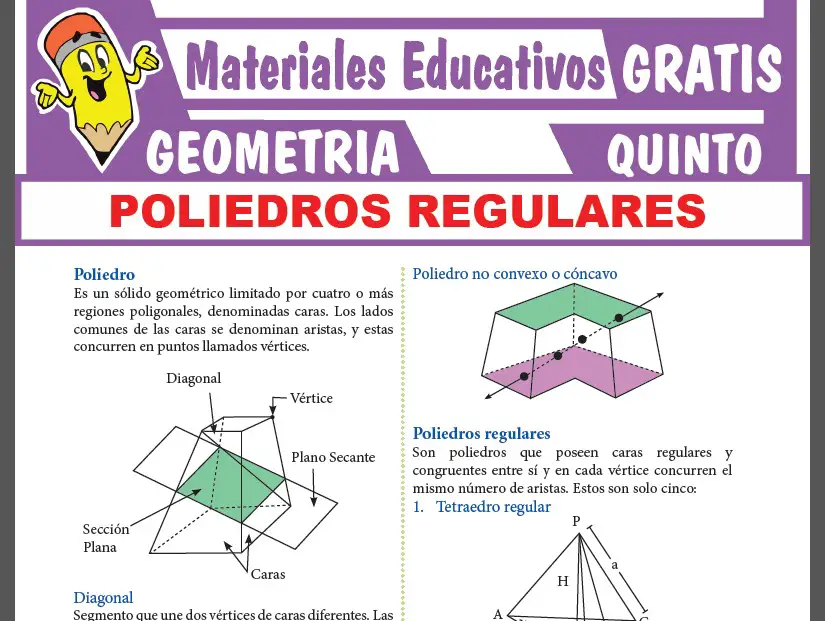
Poliedro
Es un solido geometrico limitado por cuatro o mas regiones poligonales, denominadas caras. Los lados comunes de las caras se denominan aristas, y estas concurren en puntos llamados vertices.
Diagonal
Segmento que une dos vertices de caras diferentes. Las denominacioness de los poliedros, estan en funcion al numero de caras que presenta. Asi tenemos: tetraedro (4 caras), pentaedro (5 caras), … etc.
Teorema de Euler
En todo poliedro convexo se cumple que el numero de caras mas el numero de vertices es igual al numero de aristas mas dos.
Clases de poliedros
esos son los siguientes:
Poliedros regulares
Son poliedros que poseen caras regulares y congruentes entre si y en cada vertice concurren el mismo numero de aristas.
- Tetraedro regular.
- Hexaedro regular o cubo.
- Octaedro regular.
- Dodecaedro regular.
- Poliedro regular: limitado por doce regiones pentagonales regulares congruentes.
- Icosaedro regular: Poliedro regular que presenta veinte regiones triangulares equilateras congruentes.
Ejercicios de la Ficha de Poliedros Regulares
En esta ficha educativa también encontraras muchos problemas y ejercicios de Clases de Poliedros preparadas de forma especial para los estudiantes de 5to de secundaria.
Ahora te presentaremos algunos de estos ejercicios:
- Si la arista de un tetraedro regular mide 8 u, calcula la longitud de la altura de la cara.
- Calcula el area de la region sombreada, si ABCD – EFGH es un hexaedro regular.
- En un octaedro regular, la distancia de un vértice al baricentro de la cara opuesta a dicho vértice mide 6 m. calcula el area de la superficie total de dicho solido.
- En un octaedro regular, la distancia de un vértice al baricentro de la cara opuesta a dicho vértice mide 8 cm. Calcula la longitud de la diagonal de dicho octaedro.
- Calcula el area de la region sombreada, si ABCD – EFGH es un cubo.
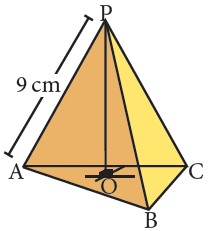
- Se tiene un tetraedro regular O – ABC, si la distancia de un vertice O al baricentro de la cara opuesta G mide 12 m. Calcula la distancia de dicho vertice a la interseccion de las alturas del triangulo AOM (M: Punto medio de BC).
Estos ejercicios y problemas de Clases de Poliedros fueron planteados por un equipo de docentes especialistas de esta área (Geometría), por lo que recomendamos a los estudiantes que desarrollen todos estos problemas propuestos.
Te invitamos a seguir navegando en nuestra web: “materialeseducativos.org”, tenemos una gran variedad de materiales educativos de todos los cursos y para todos los grados.
Más Fichas de Geometría para Quinto de Secundaria
En este sitio web educativo encontraras otras 28 fichas educativas de Geometría de los demás temas preparados para estudiantes de Quinto de Secundaria, si deseas conocer los temas que te ofrecemos, puedes revisar el siguiente enlace:
▷ ▷ 28 Fichas de Geometría para Quinto Grado ◁ ◁
Si deseas mas materiales educativos de Geometría para que descargues de manera gratuita en formato PDF y WORD, puedes revisar el siguiente enlace:
Otras Fichas de Geometría de 5to Grado
Puedes dejarnos un comentario en la parte de abajo acerca de este material educativo de Geometría para Quinto Grado.
