Aquí encontraras la ficha de Introducción a los Conjuntos para Segundo Grado de Secundaria o estudiantes que tengan 13 años de edad. Este material educativo corresponde al curso de ARITMÉTICA y lo podrás descargar GRATIS en formato PDF.
Muestra del Material Educativo
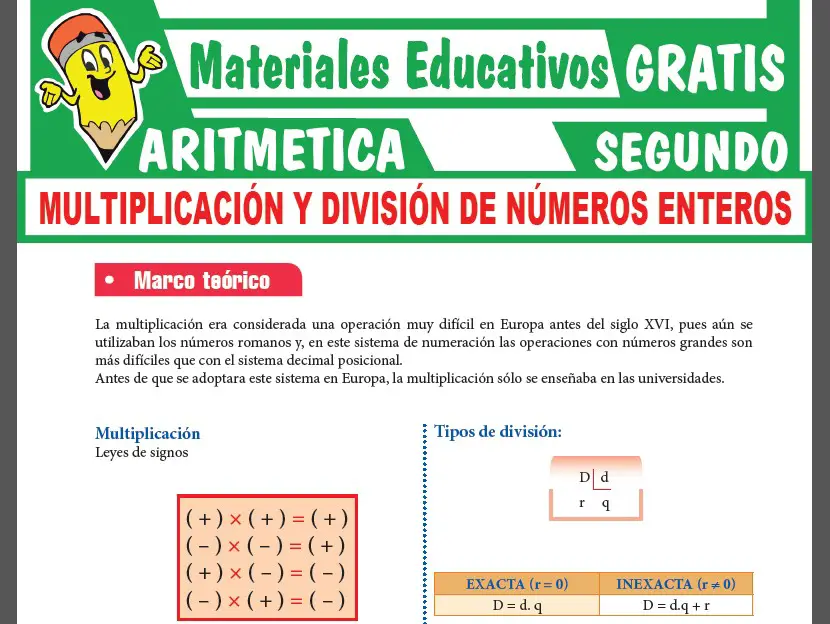
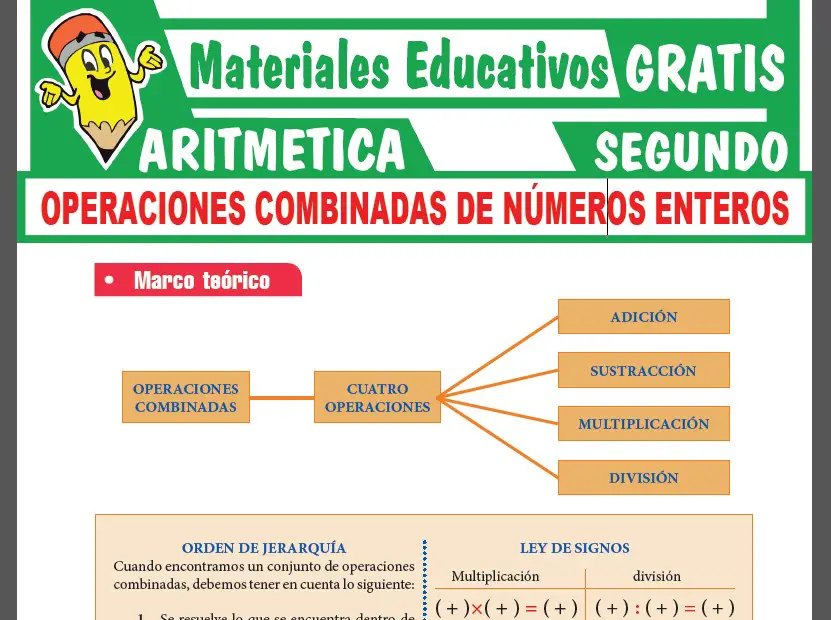
En esta parte veras una muestra de la 1era PÁGINA de la ficha de Introducción a los Conjuntos.
Para obtener este increíble material educativo de Introducción a los Conjuntos solo bastara un click, en los enlaces que te presentaremos a continuación:
Descarga GRATIS esta Ficha Educativa
Aquí podrás descargar este maravilloso material educativo de Introducción a los Conjuntos que fue elaborado para estudiantes de segundo de secundaria.
Opción A – PDF | Opción B – PDF
¿Qué Contiene esta Ficha Educativa que te Ofrecemos?
Esta ficha educativa de conjuntos que te compartimos contiene temas que muy importantes como:
- Introducción a los conjuntos
- Idea de conjunto.
- Relación de pertenencia.
- Determinación de conjuntos.
- Cardinal de un conjunto.
- Conjuntos especiales.
- Actividades para desarrollar.
Ahora te presentaremos algunos de estos conceptos:
Introducción a los Conjuntos
La teoría de conjuntos es una división de las Matemáticas que estudia los conjuntos. El primer estudio formal sobre el tema fue realizado por el matemático alemán Georg Cantor, Gottlob Frege y Julius Wilhelm Richard Dedekind en el Siglo XIX y más tarde reformulada por Zermelo.
La teoría de conjuntos fue creada por Georg Cantor, aunque George Boole dio los primeros pasos en su libro Investigations of the Laws of thought. El concepto de infinito fue tratado por Zenón de Elea y sus célebres paradojas como la de Aquiles y la tortuga.
Idea de Conjunto
El concepto conjunto, es una noción primitiva intuitiva y por consiguiente, no se puede definir. En la vida diaria usamos palabras tales como colección, grupo, conjunto:
- Una colección de libros
- Un conjunto de sillas
- Un grupo de muchachos
Notación de un Conjunto
Es convenio denotar los conjuntos con letras mayúsculas y sus elementos con letras minúsculas u otros símbolos. Para representar simbólicamente, se escriben sus elementos entre llaves y separados por comas o por un punto y coma.
Ejemplos:
- A = {enero, febrero, marzo}
- B = {a, e, i, o, u}
- C = {Ω, £, µ, ∞}
Relación de Pertenencia (∈)
Si a es un elemento del conjunto A, se denota a ∈ A y se lee: el elemento a pertenecer al conjunto A. La negación de a ∈ A es a ∉ A y se lee: el elemento a no pertenece al conjunto A.
Ejemplo:
Dado el conjunto R = {1; a; c; Ω; a}, entonces:
- a ∈ R
- b ∉ R
- Ω ∈ R
- b ∉ R
Determinación de Conjuntos
los conjuntos se pueden determinar de las siguientes formas:
Por extensión (forma tabular o enumerativa)
Se determina nombrando todos sus elementos.
- A = {0; 2; 4; 6; 8; 10}
Por comprensión (método implícito o descriptivo)
Se determina enunciando una característica común a todos sus elementos.
- A = {2x/x ∈ Z; 0 ≤ x ≤ 5}
Cardinal de un Conjunto
En términos prácticos, se llama cardinal de un conjunto A, al número de elementos no repetidos de A y se denota por n(A).
Conjuntos Especiales
Son los siguientes:
Conjunto vacío
Es aquel conjunto que carece de elementos. Se denota por φ o { }.
Conjunto unitario o Singleton
Es aquel conjunto que tiene un solo elemento.
Conjunto universal
Es aquel conjunto de todos los elementos que habrá de analizarse en un problema propuesto.
Actividades de la Ficha de Introducción a los Conjuntos
En esta ficha educativa también encontraras ejercicios de conjuntos que los estudiantes de segundo grado de secundaria podrán resolver con la ayuda del docente o padre de familia.
Estos son algunos enunciados de ejercicios de la ficha:
- El conjunto que determina por comprensión al conjunto R = {1; 3; 5; 7; 9} es:
- Se conoce que R = {r, o, n, a, l, d}; C = {c, y, n, t, h, i, a} y M = {a, r, i, t, m, e, t, i, c, a}. Calcula:
- Indica el n(A) si: A = {x2 + 1 / x ∈ Z, –1 ≤ x ≤ 3}
- Indica el n(B) si: B = {x + 5 / x ∈ N, –6 ≤ x ≤ 1}
- Si el conjunto R es unitario, calcula (a)(b) en: B = {a + 2b; 3b – a + 2; 11}
- Determina por comprensión el siguiente conjunto: A = {5; 8; 11; 14; 17}
- Dados los conjuntos unitarios M y N, calcula el valor de a. M = {a + b, 12} y N = {a – b; 6}
- Determina la suma de elementos de: M = {3x – 2 ∈ N/5 < 2x + 1 < 9}
- Calcula la suma de elementos de: C = {2x + 1 ∈ N / 11 < 3x – 1 < 23}
Este tema de conjuntos corresponde al curso de ARITMÉTICA y fue creado especialmente para estudiantes de segundo de secundaria.
En nuestra página web “materialeseducativos.org” contamos con más fichas educativas de este y otros curso y para todos los grados, te invitamos a revisarlos y descargarlos.
Más Fichas de Aritmética para Segundo de Secundaria
En nuestra pagina web también podrás encontraras otras 28 fichas de Aritmética para estudiantes de segundo de secundaria, aquí le dejamos el enlace para que lo puedas revisar:
▷ ▷ 28 Fichas de Aritmética para Segundo Grado ◁ ◁
Si necesita mas materiales educativos de aritmética para estudiantes de este mismo grado, en seguida te compartiremos el enlace de otro sitio web educativo que también te ofrece materiales educativos gratuitos de aritmética, este es su enlace:
Otras Fichas de Aritmética de 2do Grado
¿Que te pareció esta ficha educativa de aritmética para segundo grado?, coméntanos abajo (en la caja de comentarios).
